تاريخ الألعاب المنطقية - ج1

فئة : مقالات

22 يوليو 2025 بقلم هيثم السيد قسم: الفلسفة والعلوم الإنسانية

حجم الخط -18+ للنشر:

تاريخ الألعاب المنطقية - ج1

مقدمة

لا شك أن الوسائل والألعاب التعليمية المنطقية قد أدت دورًا حاسمًا في تشكيل طريقة تعلمنا وتفكيرنا، بدءاً بألعاب الطاولة القديمة وصولاً إلى التطبيقات الرقمية الحديثة. وقد تطورت هذه الأدوات، المتجذرة في قرون من البحث الفلسفي والاستكشاف الرياضي، من ألغاز ووسائل ميكانيكية بسيطة إلى منصات تفاعلية متطورة مصممة لتطوير مهارات التفكير المنطقي وحل المشكلات والتفكير النقدي. والحق أن تلك الوسائل التعليمية والألعاب المنطقية لا تكمن جاذبيتها في قدرتها على الترفيه فحسب، بل أيضًا في قدرتها على تحفيز النمو الفكري وصقل المهارات لدى جميع الفئات العمرية. ومع استدامة الاحتياج إلى تبني الابتكار في منهجيات التعلم والتدريب، تتضح أهمية الألعاب والوسائل المنطقية بشكل متزايد - ليس فقط كأدوات تكميلية، بل كمكونات أساسية في تعزيز العقول التحليلية في عالم متزايد التعقيد. يستكشف الجزء الأول من هذا المقال التاريخ الثري للوسائل والألعاب التعليمية المنطقية، ويتتبع تطورها، ليُبرز أهميتها المتزايدة في المشهد التعليمي الراهن.

ما هو المنطق؟ وما هي مهاراته؟

المنطق هو علم التفكير الصحيح، وموضوعه هو الاستدلال inference، أي الانتقال من مقدمات فُرضت صحتها إلى نتيجة تلزم عنها.(1) يستلزم الاستدلال المنطقي مهارات متنوعة، منها الاستنباط deduction والاستقراء induction. والاستنباط، أو التفكير الاستنباطي، وفقاً لـ استينبرغ (2017)، هو الوصول إلى نتيجة بشأن حالات محددة بواسطة تعميمات أو مقدمات عامة تتعلق بهذه الحالات.(2) أما الاستقراء، أو التفكير الاستقرائي inductive reasoning، وهو بيت القصيد في سياقنا الراهن، وفقاً لـ كلاور (2008) هو الوصول إلى، أو الكشف عن، تعميمات أو قواعد أو انتظام ما بواسطة مقدمات تتعلق بحالات محددة. مثلا، عندما يُقدَّم لك عدد من الأشياء وتجد أن كل هذه الأشياء هي من فئة الألعاب الخشبية فإنك بذلك قد وصلت إلى تعميم أو انتظام عبر ادراكك لعلاقة تربط بين هذه الأشياء.(3) وعلى هذا، يُعرِّف سبيرمان (1932) العمليات الاستقرائية بأنها "تعليم العلاقات" education of relations.(4)

وحول قيمة وأهمية مهارة الاستقراء في التفكير الإنساني، يؤكد ثورستون عبر بحوث أجراها في عام 1938 أن الاستقراء هو أصل التفكير، أو هو العوامل الفكرية المركزية التي نطلق عليها "تفكير" reasoning.(5) بل يصفه كاتيل (1963) بأنه "الذكاء الحاد" fluid intelligence.(6) فضلا عن هذا، إن مهارات التفكير الاستقرائي هي متطلب أساسي مسبق لحل المشكلات، لاسيما المعقدة. وعلى هذا، اهتمت العديد من الدراسات التجريبية بالبحث في مدى أهمية تعلم المهارات الاستقرائية بالممارسة knowing-by-doing عبر تطبيق مقاربة "التعلم باللعب" playing-based learning. أذكر منها، دراسة أُجريت في عام (2008) على ما يقرب من 3600 متدرب عبر استخدام 74 تجربة تدريبية، والتي أثبتت أن التدريب على استراتيجية التفكير الاستقرائي (تعليم العلاقات) بالممارسة يُحسِّن الأداء المعرفي أو الادراكي من حيث: (أ) زيادة معدل الذكاء الحاد والأداء، و(ب) تعلم أكاديمي أفضل لموضوعات التخصص.(7) ومن هنا، مست الحاجة إلى ابتكار وسائل تعليمية منطقية تدعم تحقيق هذه الأهداف.

نشأة الألعاب المنطقية

إن فكرة تصميم واستخدام وسائل وألعاب منطقية لأغراض تعليمية تهدف إلى تعليم وتطوير وممارسة مهارات التفكير المنطقي المتنوعة (مثل التحليل والتركيب) هي فكرة قديمة-حديثة يمكن العودة بها إلى المفكر والرياضي اليوناني أرخميدس (287-212 ق.م) والذى قدم أول لغز تعليمي عرفه التاريخ، المعروف باسم مربع أرخميدس أو أوستوميشين Ostomachion.(8) كما يتضح من شكل (1)، يتكون مربع أرخميدس من 14 قطعة الهدف منها هو إعادة تجميع هذه القطع لتشكيل مربعات متنوعة يصل عددها إلى حوالي 536 مربع مختلف.

شكل (1): مربع أرخميدس

بيانو المنطق logic piano هو نموذج آخر للوسائل التعليمية المنطقية التي قدمها المنطقي الإنجليزي وليام جيفونز (1882-1835) في القرن التاسع عشر. كما يتضح من شكل (2)، تتألف وسيلة جيفونز من شيء شبيه بالبيانو في وضع رأسي لا أفقي، وتحوى قطعاً خشبية مثبتاً عليها حروف الهجاء ورموزاً للرابطة المنطقية وأداة الفصل وكلها في ترتيب معين وعلى نحو يسهل تحريكها باليد. يمكنك بفضل هذه الوسيلة الوصول إلى التركيبات المنطقية الممكنة بين الحدود التي تؤلف أي عدد من المقدمات. صمم جيفونز وسيلته في عام 1869 وتحدث عنها في محاضرة ألقاها أمام "الجمعية الملكية" Royal Society وقدمها لأعضاء هذه الجمعية في 20 يناير 1870.(9) وعلى الرغم من أن هدف جيفونز كان هدفاً تعليمياً، إلا أن بيانو المنطق استُخدم فيما بعد ليكون نواة للحاسوب، حيث كانت الآلة الأولى ذات القوة الكافية لحل مشكلة معقدة أسرع من المشكلة التي يمكن حلها دون مساعدة الآلة. (10)

شكل (2): بيانو المنطق

الألعاب المنطقية حديثاً

وحول بعض الاسهامات الحديثة في اختراع وسائل وألعاب منطقية تعليمية، وعبر البحث في قاعدة بيانات المنظمة العالمية للملكية الفكرية (ويبو) WIPO تبين وجود عدد من الاختراعات السابقة في الفترة (1980-2009)، ووصفها على النحو التالي:

Berrebi Meyer, Logical deduction Development Game, US4222565-16.09.1980

هذا الاختراع هو لعبة تعليمية تهدف إلى تطوير مهارات "التفكير الاستنباطي" عند اللاعبين، وخاصة الأطفال. تتكون هذه اللعبة من وجهين: يحتوى الوجه الأول على مجموعة من التجميعات المرتبة في مربعات لكل منها قيمة منطقية 0 أو 1، أو قيمة محايدة قد تكون مساوية لـ 0 أو 1 وفقًا للظروف، كما تشتمل جميع التجميعات المرتبة على نفس العدد n من المربعات، ويحتوى الوجه الآخر على مجموعة من العناصر المتحركة مثل القطع والعدادات والكتل والأقراص، إلخ، مع وجود وجه واحد على الأقل لكل منها يرتبط بالقيمة المنطقية 0 أو القيمة المنطقية 1. والهدف هو أن تكون قيم مربعات التجميع المكونة من العناصر المتنقلة في علاقة منطقية محددة مع قيم مربعات تجميعات النماذج.(11)

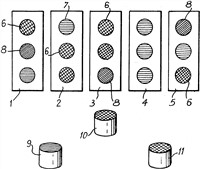
شكل (3): لعبة ماير

Laisure Thomas, Educational Board Game for Teaching Mathematics and Logic, US4883277-28.11.1989

هذا الاختراع هو لعبة تعليمية لوحية تهدف إلى تطوير مهارات "التفكير الاستنباطي" عند اللاعبين. يحاول اللاعبون التنبؤ بعدد من الدلائل (الأشكال الهندسية) التي سيتم الكشف عنها في مجموعة ما من الدلائل بعد رؤية أقل عدد من إجمالي الدلائل في المجموعة.(12)

شكل (4): لعبة توماس

Morse H. Ogden, Vocabulary Acquisition Using Structured Inductive Reasoning, US6120297-19.09.2000

هذا الاختراع هو وسيلة تعليمية "حاسوبية" لزيادة المفردات اللغوية عند الطالب باستخدام "التفكير الاستقرائي". يعرض النظام الحاسوبي كلمة مستهدفة ليتم تعلمها ومعلومات الاشتقاق المرتبطة بها، متبوعة بدليل. يمكن أن تتضمن معلومات الاشتقاق دليل النطق، ومعلومات الخلفية التاريخية أو القصصية، ومعلومات حول الجذر والبادئة. تتطلب الإجابات الصحيحة فهمًا لاشتقاق الكلمة المعنية. يتم بعد ذلك تقديم الإجابة الصحيحة للدليل وشرح هذه الإجابة. يوفر كل دليل وإجابة فهمًا إضافيًا للكلمة المستهدفة، ويصل الطالب إلى معنى فردي للكلمة من خلال الاستدلال الاستقرائي.(13)

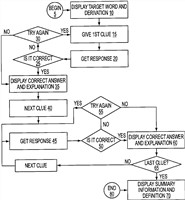
شكل (5): وسيلة أوجدن

Vass Ladislau, Logic Game, RO117508-30.04.2002

هذا الاختراع هو لعبة منطقية لها خصائص تعليمية وإرشادية، تسلي المستخدمين من أي عمر فوق سن الخامسة. وفقًا للاختراع، تتكون اللعبة المنطقية من لوحة ألعاب مُوزع عليها عدد من الصناديق N. يوضع في كل صندوق عدد من الأقراص مختلفة الأقطار. تعمل هذه الأقراص بمفاتيح كهربائية مثبتة أسفل الصناديق وتضئ باللون الأخضر عندما تكون مرتبة بشكل صحيح في الأقفاص في وضع أفقي، بينما عندما تُرتب الأقراص في وضع عمودي، تضاء المساحة (المساحات) باللون الأحمر.(14)

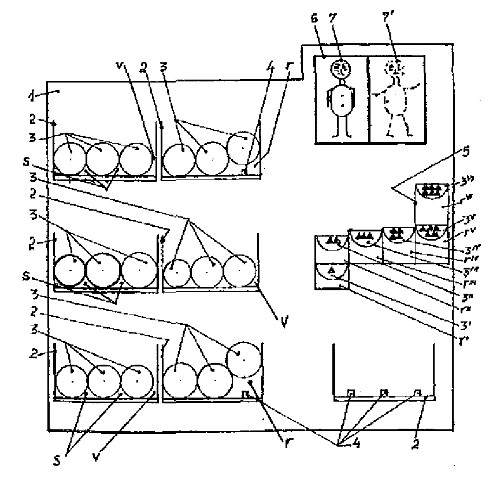
شكل (6): لعبة فاس

Rosenqvist Sakari, Logic Game, WO/2009/063126-22.05.2009

هذا الاختراع هو لعبة منطقية متعددة الأوجه (تكعيبية) للأغراض التعليمية. تتكون من عنصرين أو أكثر من عناصر اللعبة في كل وجه، حيث توضع علامة مرئية واحدة أو أكثر لكل عنصر من عناصر اللعبة. والهدف هو ترتيب عناصر اللعبة بطريقة يتم فيها تنفيذ منطق العلامات الموجودة على الوجوه المتوازية لعناصر اللعبة المتجاورة و / أو المتتالية.(15)

شكل (7): لعبة ساكاري

إضافة إلى هذه النماذج، يوجد عدد من الاختراعات التي تتخذ من عبارة "لعبة منطق" logic game عنواناً لها، إلا أن مثل هذه الألعاب ليست سوى مثير عقلي mind teaser. مثل، US5261668 (1993), US20180161667 (2018) وليست وسائل أو ألعاب منطقية تعليمية تستهدف تطوير وممارسة مهارات محددة في التفكير المنطقي.

بناء على ذلك، يتضح أنه على مدار الثلاثين عام الماضية (1980-2009) اخترعت خمس ألعاب منطقية تعليمية فقط على مستوى العالم؛ أي بمعدل اختراع لعبة واحدة كل 6 سنوات. أضف إلى هذا، التباعد الزمنى الشديد بين كل اختراع وآخر. ويكفى أن أشير إلى وجود فجوة زمنية بعيدة بين وقتنا الراهن وآخر لعبة منطقية تعليمية اخترعت (12 سنة تقريباً).

ألعاب منطقية عربية

نظراً للندرة الشديدة في وجود مثل هذه النوعية من الألعاب التعليمية في مجال التفكير المنطقي، لاسيما في عالمنا العربي، مست الحاجة إلى العمل على ابتكار ألعاب منطقية بعقل عربي تسهم في تطوير هذا المسار التعليمي المهم، وهو "التعلم القائم على اللعب" game-based learning لاسيما في مجال تطوير مهارات التفكير المنطقي عند طلاب المدارس والجامعات.

أختم هذا الجزء بتعريف بلعبة منطقية عربية مبتكرة تضاف إلى تاريخ الألعاب المنطقية السابق، وهى لعبة رونري Ronri التعليمية. هذا الاختراع هو وسيلة ولعبة منطقية تعليمية تهدف إلى تطوير مهارات التفكير المنطقي الاستقرائي عند مستخدميها من أي فئة عمرية ما فوق الخمس سنوات. تتكون هذه اللعبة من ثلاثة أشكال رئيسة (دائرة، مربع، مستطيل). يحتوى كل شكل رئيس على 8 وحدات أو أشكال جزئية، بإجمالي 24 وحدة. تحتوى كل وحدة على عدد من المعطيات (ألوان، أحجام، أشكال رسومية، كلمات، وأرقام). طريقة اللعب هي أن تجد الصفة أو الخاصية أو العلاقة التي تربط بين كل وحدة أو كل معطى وباقي الوحدات أو المعطيات، ومن ثم التعميم عبر إدراج هذه الوحدات أو هذه المعطيات ذات الصفة أو العلاقة المشتركة في مجموعة تميزها عن باقي الوحدات. تحتوى هذه اللعبة على 23 تعميم أو قاعدة تصنيف (على الأقل)، يندرج تحتها 75 مجموعة. ومن ثم، تقدم هذه اللعبة 23 محاولة (على الأقل) للممارسة والتدريب، عبر تدرج في مستويات الصعوبة (سهل، متوسط، صعب).

شكل (8): لعبة رونري

أتناول في الجزء الثاني من هذا المقال عدد من ألعاب البطاقات المنطقية بوصفها صورة أخرى من صور ألعاب التفكير المنطقي، ومدى إسهامنا نحن العرب في تطوير ألعاب بطاقات منطقية.

خاتمة

يعكس التطور التاريخي لألعاب المنطق التعليمية سعي البشرية الدؤوب نحو المعرفة والتفكير المنطقي والتحدي الفكري. تعد هذه الأدوات، التي تتجاوز كونها مجرد تسلية ترفيهية، أدوات تعليمية فعّالة تُنمّي التفكير النقدي، وتُحسّن القدرات المعرفية، فضلا عن تهيئة المتعلمين للتعامل مع المشكلات المعقدة في السياقات الأكاديمية والمهنية واليومية. في ظل سعي أنظمة التعليم حول العالم إلى تنمية مفكرين أكثر تفاعلاً وتحليلاً وابتكاراً، أصبح دور ألعاب ووسائل المنطق التعليمية أكثر أهمية من أي وقت مضى. إن تبني هذه الأدوات لا يُكرّم تراثًا فكريًا ثريًا فحسب، بل يُمهّد الطريق أيضًا لتجارب تعليمية أكثر فعالية وديناميكية في المستقبل.

مصادر وهوامش:

See: Nunes T. (2012) Logical Reasoning and Learning. In: Seel N.M. (eds) Encyclopedia of the Sciences of Learning. Springer, Boston, MA.
Steinberg E. (2017) Deductive Reasoning. In: International Encyclopedia of Communication Research Methods. Wiley-Blackwell.
Karl Josef Klauer, Gary D. Phye (2008), Inductive Reasoning: A Training Approach, Review of Educational Research March 2008, Vol. 78, No. 1, pp. 85–123, p 86
Spearman, C. (1923). The nature of intelligence and the principles of cognition. London: Macmillan.
Thurstone, L. L. (1938). Primary mental abilities. Psychometric Monographs, No. 1.
Cattell, R. B. (1963). Theory of fluid and crystallized intelligence: A critical experiment. Journal of Educational Psychology, 54, 1–22
Karl Josef Klauer, Gary D. Phye (2008), Inductive Reasoning: A Training Approach, p 85
See: Rorres C. (ed) (2017). Archimedes in the 21st Century: Proceedings of a World Conference at the Courant Institute of Mathematical Sciences. Birkhäuser. Pp.66-67
انظر: محمود فهمى زيدان، المنطق الرمزى نشأته وتطوره، مؤسسة شباب الجامعة، اسكندرية، 1989، ص89.
https://patentscope.wipo.int/search/en/detail.jsf?docId=RO233907760&_cid=P22-KP9QCC-48926-1
https://patentscope.wipo.int/search/en/detail.jsf?docId=WO2009063126&tab=PCTBIBLIO